It's kind of interesting to think what function would have this as it's MacLaurin series, that at f=1 it is 0, and the first derivative there is 1, and every successive derivative is 1 more than the one before it...
It actually is (x^x)-1, see:
Tuesday, December 22, 2015
Factorial sum Maple doesn't know
Considering the sum:
But it's clear this sum should be equal to one, consider the first 7 terms:
If we were to increase the last coefficient by 1 it is exactly unity:
This is because 8/8! is 7! which adds one more 7! to 6/7! to make 7/7! which is 6!, etc.. until you have 1/2! plus 1/2! equaling 1...
It's kind of interesting to think what function would have this as it's MacLaurin series, that at f=1 it is 0, and the first derivative there is 1, and every successive derivative is 1 more than the one before it...
It actually is (x^x)-1, see:
It's kind of interesting to think what function would have this as it's MacLaurin series, that at f=1 it is 0, and the first derivative there is 1, and every successive derivative is 1 more than the one before it...
It actually is (x^x)-1, see:
Subscribe to:
Post Comments (Atom)
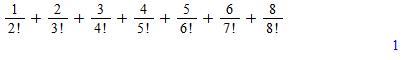
No comments:
Post a Comment