Alternate numbering system

Just considering this series, here are the first 9 terms:

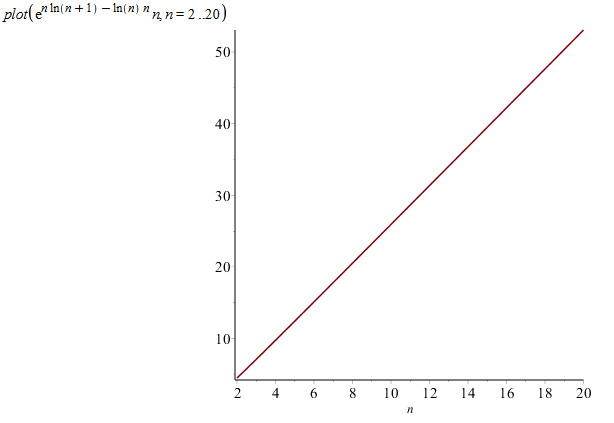
Where the next coefficient is chosen so the sum is as large as it can be not exceeding 1... The growth of the coefficients  can be solved for by noting the next term should by multiplied by some a so that it is as large as the previous term when it has a coefficient of 1...

Plotted it is linear:

So I've noticed that this series is basically as efficient for writing any number between 0 and 1 with regards to number of decimal digits as decimal itself is! By the pigeon hole principle no series can be better for getting k decimal digits than the decimal series a1/10 + a2/100...