I was thinking of a setup like this:
Basically a pump, it could be run with an engine but I show it here with a foot pump, connected through an insulative container and to an array of very thin thermally conductive tubing. there is an opening on the top of this tubing so water can fill it, but it is thin enough that when air is pumped into it the air replaces the water in the tubing without forming bubbles. It was hard to diagram but the tubing has to be arranged so when no air is coming out of the pump water can fill the tubing, so it would be more horizontal and on a slant. The volume of the tubing is the same as one cycle of the pump, let's say 1 Liter.
The operation is that the pump presses one time, forcing air to fill the tubing, which forces the water out, then as the pump is refilling with air from the outside water drains into the tubing and the air that was in the tubing exits from the exhaust tube. Then this repeats. This gradually cools the water.
The reason it cools the water is the pump has 1 liter of air and the tubing also holds 1 liter of air. But there is much more surface area over the tubing so the pressure of the air drops as it fills the tube. This is because pressure is a force per area and the force doesn't change and the area increases so the pressure drops.
by the ideal gas law:
Since n and R on the right side are constant, and the volume remains constant, if the pressure drops the temperature also has to drop. I figure for the shape of the pump and tubing the pressure could drop 1/20th so it should be efficient in it's cooling.
**Edit**
I think maybe an even better design would be with a motorized pump that's fast enough to keep the tubing from filling with water, and have the exhaust pipe connected back to entry of the pump so the same air is cooled over and over, the pump would be built so it could radiate heat well to the outside air when it pressurizes the air coming into it.
analytics
Tuesday, December 24, 2013
Tuesday, December 3, 2013
Minimum amount of energy burned to break a sweat
Looking on the internet, the specific heat of the body is about 3470 Joules/ kg*C and the body raises temperature by approximately 1 degree Celsius as you raise your core temperature through exercise to the point where you are sweating. There are also 4184 joules per dietary calorie. And there are 2.2 pounds per kilogram. So the amount of dietary calories you burn by raising your body temperature to the point where you sweat is:
3470 (Joules / kg*C) * (1 calorie/4184 Joules)(1 kg / 2.2 pounds)*(1 degree Celsius delta temperature) =
.37 (calories/pound)
So a 200 pound man burns .37*200 or 74 calories going from resting temperature to a sweat at the minimum. Really it will be higher because some of the heat generated is radiated away from the body and doesn't go towards raising the temperature of the body. Also there is an efficiency to burning calories and doing work in the physics sense, this 74 calories is just the waste heat, you will be using some calories to propel your body if your running or moving a weight if your lifting weights. Also there may be a caloric cost for the body to initiate the sweating process, I'm not sure if it's significant though.
So I believe this is why interval training works so well for losing weight, because if this 200 pound person over a period exercised to the point of sweating then let himself cool back down to normal and then repeated 10 times that would be at a minimum 740 calories. This could probably be done over an hour where you jog or run fast enough to break a sweat 10 times alternating with cooling down. Compare this to continually jogging for an hour only burns 640 calories for a 200 pound man.
I think an analogy might be to think of boiling water, it takes a very high heat to get water to a boil, but once it's boiling the heat can be turned down to maintain a boil. It may be that the body expends a lot less energy to maintain a sweat and keep the body temperature up than it does to get to that temperature in the first place. So to use the most energy you would heat the water to a boil, then cool it off, then repeat. And it seems to actually be the same for exercising that getting to a sweat through exercise then allowing your body to cool and repeating actually seemingly paradoxically uses more energy than solidly exercising over the same interval. And of course it takes a lot less effort because you are resting a good percentage of the time.
3470 (Joules / kg*C) * (1 calorie/4184 Joules)(1 kg / 2.2 pounds)*(1 degree Celsius delta temperature) =
.37 (calories/pound)
So a 200 pound man burns .37*200 or 74 calories going from resting temperature to a sweat at the minimum. Really it will be higher because some of the heat generated is radiated away from the body and doesn't go towards raising the temperature of the body. Also there is an efficiency to burning calories and doing work in the physics sense, this 74 calories is just the waste heat, you will be using some calories to propel your body if your running or moving a weight if your lifting weights. Also there may be a caloric cost for the body to initiate the sweating process, I'm not sure if it's significant though.
So I believe this is why interval training works so well for losing weight, because if this 200 pound person over a period exercised to the point of sweating then let himself cool back down to normal and then repeated 10 times that would be at a minimum 740 calories. This could probably be done over an hour where you jog or run fast enough to break a sweat 10 times alternating with cooling down. Compare this to continually jogging for an hour only burns 640 calories for a 200 pound man.
I think an analogy might be to think of boiling water, it takes a very high heat to get water to a boil, but once it's boiling the heat can be turned down to maintain a boil. It may be that the body expends a lot less energy to maintain a sweat and keep the body temperature up than it does to get to that temperature in the first place. So to use the most energy you would heat the water to a boil, then cool it off, then repeat. And it seems to actually be the same for exercising that getting to a sweat through exercise then allowing your body to cool and repeating actually seemingly paradoxically uses more energy than solidly exercising over the same interval. And of course it takes a lot less effort because you are resting a good percentage of the time.
Saturday, November 23, 2013
Even simpler idea for a proof of twin prime conjecture
The first lemma will be: "The second of a pair of twin primes does not have a remainder of 2 when divided by any prime up to its square root, and a number is the second of a pair of twin primes if it doesn't have a remainder of 2 or 0 when divided by any prime up to it's square root."
Proof: Suppose P did divide a prime p less than it's square root with a remainder of 2. Then the number 2 less than P would divide it exactly. Thus the number 2 less than P is not prime, which contradicts the fact that P was the second of a pair of twin primes. Also if P does not divide any number less than it's square root with a remainder of 0 then it is prime, and if it also does not divide any of those with a remainder of 2 then the number 2 less than P does not divide them either, which means it is also prime. Hence, P is the second of a pair of twin primes.
Theorem: Let N = (p+1)^2-1, a way to roughly count the number of primes less than N is:
N*(1/2)*(2/3)*(4/5)...*(p-1)/p
Proof: Roughly 1/2 of all the numbers up to N won't divide 2, 2/3 won't divide 3, and so on up to p-1. Whether a number divides p or divides another prime q happen independently of one another so the percentages are multiplied. (p+1)^2 is also the first number where factors of p+1 need to be considered as any number that divides p+1 evenly before that also divides a smaller prime.
Theorem 2: Let N = (p+1)^2-1, a way to count one of each of every pair of twin primes less than N is roughly:
N*(1/2)*(1/3)*(3/5)...*(p-1)/p: The same as the formula from theorem 1 but the numerators of all but the 1/2 term are decreased by 1.
Proof: Because of the lemma, we know that numbers that have a non-zero remainder when divided by every p up to the square root, and also not 2 when divided by each p are one of a pair of twin primes. For every p but 2 this is one less possible remainder so every term other than 1/2's numerator is reduced by 1. For example there are 3 possibilities for the remainder when divided by 5, 1,3, and 4. So 3/5 appears in the fraction. This formula thus roughly counts the number of twin primes less than N.
Theorem 3: There are an infnite number of twin primes estimated by the formula in Theorem 2:
Proof: Suppose the number of twin primes up to N used theorem 2's formula and counted P pairs of twin primes by:
((p)^2-1)*(1/2)*(1/3)*(3/5)...*(p-2)/p
for now we can write that as:
((p)^2-1)*X
We can show that if we replace p with the next bigger prime q, the number of twin primes estimated always increases because the ratio of estimated primes is:
This ratio is always greater than 1 as p gets larger because the ratio of q^2-1 to p^2-1 is larger than 1 by more than the ratio of (q-2) to q is smaller than 1. This means there must be a positive number of estimated pairs of twin primes between p^2-1 and q^2-1 And since there are an infinite number of primes to choose p and q from there must be an infinite number of pairs of twin primes...
Proof: Suppose P did divide a prime p less than it's square root with a remainder of 2. Then the number 2 less than P would divide it exactly. Thus the number 2 less than P is not prime, which contradicts the fact that P was the second of a pair of twin primes. Also if P does not divide any number less than it's square root with a remainder of 0 then it is prime, and if it also does not divide any of those with a remainder of 2 then the number 2 less than P does not divide them either, which means it is also prime. Hence, P is the second of a pair of twin primes.
Theorem: Let N = (p+1)^2-1, a way to roughly count the number of primes less than N is:
N*(1/2)*(2/3)*(4/5)...*(p-1)/p
Proof: Roughly 1/2 of all the numbers up to N won't divide 2, 2/3 won't divide 3, and so on up to p-1. Whether a number divides p or divides another prime q happen independently of one another so the percentages are multiplied. (p+1)^2 is also the first number where factors of p+1 need to be considered as any number that divides p+1 evenly before that also divides a smaller prime.
Theorem 2: Let N = (p+1)^2-1, a way to count one of each of every pair of twin primes less than N is roughly:
N*(1/2)*(1/3)*(3/5)...*(p-1)/p: The same as the formula from theorem 1 but the numerators of all but the 1/2 term are decreased by 1.
Proof: Because of the lemma, we know that numbers that have a non-zero remainder when divided by every p up to the square root, and also not 2 when divided by each p are one of a pair of twin primes. For every p but 2 this is one less possible remainder so every term other than 1/2's numerator is reduced by 1. For example there are 3 possibilities for the remainder when divided by 5, 1,3, and 4. So 3/5 appears in the fraction. This formula thus roughly counts the number of twin primes less than N.
Theorem 3: There are an infnite number of twin primes estimated by the formula in Theorem 2:
Proof: Suppose the number of twin primes up to N used theorem 2's formula and counted P pairs of twin primes by:
((p)^2-1)*(1/2)*(1/3)*(3/5)...*(p-2)/p
for now we can write that as:
((p)^2-1)*X
We can show that if we replace p with the next bigger prime q, the number of twin primes estimated always increases because the ratio of estimated primes is:
This ratio is always greater than 1 as p gets larger because the ratio of q^2-1 to p^2-1 is larger than 1 by more than the ratio of (q-2) to q is smaller than 1. This means there must be a positive number of estimated pairs of twin primes between p^2-1 and q^2-1 And since there are an infinite number of primes to choose p and q from there must be an infinite number of pairs of twin primes...
Idea for a simple proof of twin prime conjecture?
Suppose you do a similar operation to the sieve of Eratosthenes, but mark off numbers that are p*n+2 numbers for n greater than 1 instead of p*n numbers. You would start with the list of numbers to infinity...
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28...
Mark off all the 2*n+2 numbers...
1,2,3,4,5,x,7,x,9,x,11,x,13,x,15,x,17,x,19,x,21,x,23,x,25,x,27,x...
Of those mark off the 3*n+2 numbers with n greater than 1...
1,2,3,4,5,x,7,x,9,x,x,x,13,x,15,x,x,x,19,x,21,x,x,x,25,x,27,x..
and so on until you get...
1,2,3,4,5,x,7,x,9,x,x,x,13,x,15,x,x,x,19,x,21,x,x,x,25,x, x, x...
Now there are 3 things we know about this list...
1.The total number of entries up to n is n/log(n) because one number was marked off for every one number marked off in the usual sieve of Eratosthenes, and the prime number theorem states that in the usual sieve the number of numbers left will be n/log(n).
2.The list of these numbers continues indefinitely because n/log(n) continues to increase to infinity.
3. Every number on this list is 2 more than a prime, except for 3. This follows because every number we've marked off is two numbers to the right of the number we would mark off in the normal sieve of Eratosthenes. So what would be left as primes after doing the normal sieve we are left with numbers that are two to the right of those.
Now we can deduce that there will always be primes left on this modified sieve of Eratosthenes because the remainders when a prime is divided by all the primes up to the square root are equally likely, so clearly an infinite number of them will have a different remainder than 2 when divided by each prime up to the square root. But these primes are all the second prime of a pair of twin primes by fact number 3 above. So thus there are an infinite number of twin primes.
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28...
Mark off all the 2*n+2 numbers...
1,2,3,4,5,x,7,x,9,x,11,x,13,x,15,x,17,x,19,x,21,x,23,x,25,x,27,x...
Of those mark off the 3*n+2 numbers with n greater than 1...
1,2,3,4,5,x,7,x,9,x,x,x,13,x,15,x,x,x,19,x,21,x,x,x,25,x,27,x..
and so on until you get...
1,2,3,4,5,x,7,x,9,x,x,x,13,x,15,x,x,x,19,x,21,x,x,x,25,x, x, x...
Now there are 3 things we know about this list...
1.The total number of entries up to n is n/log(n) because one number was marked off for every one number marked off in the usual sieve of Eratosthenes, and the prime number theorem states that in the usual sieve the number of numbers left will be n/log(n).
2.The list of these numbers continues indefinitely because n/log(n) continues to increase to infinity.
3. Every number on this list is 2 more than a prime, except for 3. This follows because every number we've marked off is two numbers to the right of the number we would mark off in the normal sieve of Eratosthenes. So what would be left as primes after doing the normal sieve we are left with numbers that are two to the right of those.
Now we can deduce that there will always be primes left on this modified sieve of Eratosthenes because the remainders when a prime is divided by all the primes up to the square root are equally likely, so clearly an infinite number of them will have a different remainder than 2 when divided by each prime up to the square root. But these primes are all the second prime of a pair of twin primes by fact number 3 above. So thus there are an infinite number of twin primes.
Thursday, November 21, 2013
Josephus Crypto
So suppose you have a message that you want to encrypt M. I'll just show a short one:
watson come here i need you
i mean if you have a minute
The basic idea I had was that you take the length of message M, n, which in this case is 54, and generate a key K which can be any number significantly greater than L. For this example it will be 386. Then to find the first letter of the new message find the 386th letter of the message modulo L. 386 mod 54 is 8. The eighth letter of the message (first letter is letter 0) is the o in "come" which becomes the first letter of the new message S.
o
Now the letter that was chosen is removed from the original message to generate M2.
watson cme here i need you
i mean if you have a minute
To get the second letter of the new message start with the next letter after the one removed and count to the 386th letter after that this time modulo 53 because there are 53 letters in the message. Mathematically that is (7+386) mod 53 = 22 (remember it is a 7 instead of an 8 because the first letter is letter 0). The 22th letter of the message is the space before the first y so that becomes the second letter of the new message S and this whole process iterates until all the letters from M are now in S.
o eenuwham su nem i euia
i eea v aefdmiyoronynhtoct
python code:
def main():
M = "watson come here i need you i mean if you have a minute"
S = ""
K = 386
p = 0
while len(M) > 1:
i = (p+K)%(len(M)-1)
S+=M[i]
M = M[:i] + M[(i+1):]
print(S)
main()
To decode, start with an empty string and build it up in reverse.
The name:
It's related to the Josephus problem which is based on a historical occurrence:
http://en.wikipedia.org/wiki/Josephus_problem
It's sort of a different dimension to cryptography, that instead of scrambling the value of the characters as the starting point you scramble the order that they appear. But you could also combine both...
watson come here i need you
i mean if you have a minute
The basic idea I had was that you take the length of message M, n, which in this case is 54, and generate a key K which can be any number significantly greater than L. For this example it will be 386. Then to find the first letter of the new message find the 386th letter of the message modulo L. 386 mod 54 is 8. The eighth letter of the message (first letter is letter 0) is the o in "come" which becomes the first letter of the new message S.
o
Now the letter that was chosen is removed from the original message to generate M2.
watson cme here i need you
i mean if you have a minute
To get the second letter of the new message start with the next letter after the one removed and count to the 386th letter after that this time modulo 53 because there are 53 letters in the message. Mathematically that is (7+386) mod 53 = 22 (remember it is a 7 instead of an 8 because the first letter is letter 0). The 22th letter of the message is the space before the first y so that becomes the second letter of the new message S and this whole process iterates until all the letters from M are now in S.
o eenuwham su nem i euia
i eea v aefdmiyoronynhtoct
python code:
def main():
M = "watson come here i need you i mean if you have a minute"
S = ""
K = 386
p = 0
while len(M) > 1:
i = (p+K)%(len(M)-1)
S+=M[i]
M = M[:i] + M[(i+1):]
print(S)
main()
To decode, start with an empty string and build it up in reverse.
The name:
It's related to the Josephus problem which is based on a historical occurrence:
http://en.wikipedia.org/wiki/Josephus_problem
It's sort of a different dimension to cryptography, that instead of scrambling the value of the characters as the starting point you scramble the order that they appear. But you could also combine both...
Wednesday, November 6, 2013
Good approximation for Gauss's circle problem
I found this formula as an approximation to Gauss's circle problem that I described on the last blog entry:
A comparison of the output of this above to the actual values:
r= 0: 0 ~ 1
r=1: 2 ~ 5
...
r=10: 310.45 ~317
r=20: 1251.38 ~1257
r=30: 2820.99 ~2821
r=40: 5019.11 ~5025
r =45: 6353.84 ~6361
(within .1 % on that last one)
I only found one example where it overestimates:
r=46 6639.63 ~6625
proof: Actually I'm not sure why, but this expression is exact:
A comparison of the output of this above to the actual values:
r= 0: 0 ~ 1
r=1: 2 ~ 5
...
r=10: 310.45 ~317
r=20: 1251.38 ~1257
r=30: 2820.99 ~2821
r=40: 5019.11 ~5025
r =45: 6353.84 ~6361
(within .1 % on that last one)
I only found one example where it overestimates:
r=46 6639.63 ~6625
proof: Actually I'm not sure why, but this expression is exact:
because r^2-a^2 is the height of the circle in one quadrant as a increases and the floor of that height counts the number of grid points less than that height then you multiply that by 4 and add the points on the axes with the 4*r term and add one for the point in the very center.
and then I used the fact that the average value before flooring is probably .5 to get the approximation
Gauss's circle problem calculation without using the floor function
Gauss's circle problem is the one that asks given a circle of a certain radius centered at the origin, how many grid points are on the circle or inside of it. For example:
The graphic shows the answers for radius = 1, 2, 3 are 5, 13, 29 respectively.
One way to calculate how many there would be is to add 1 for every point on the grid where the distance to the center is greater than the radius, and count how many times that happens checking every grid point. But that's really more of an algorithm...
I found this other way:
My reasoning was, if you look at the bottom right quadrant of the circle in question (disregarding the points on the axis) and and imagine all the vectors from those points to the point on the circle along the line to the origin, you see vectors like this:
It ends up you can always tell from the sign of the y component of this vector whether the point in question is inside or outside of the circle. The X above is the expression for the y component of this vector, derived by calculating the angle to a point from the origin and then finding the polar coordinates of a point that is that same angle from the origin but with a distance to the origin r, of the radius of the circle, and then converting back to cartesian coordinates and looking at the y component. I divide whatever this y value is by the absolute value to get either 1 if the point is inside the circle, 0 if it is on the circle, or -1 if it is outside.
The final expression is totalling these values up and solving for how many must be inside the whole circle from that sum.
Unfortunately it's harder to get rid of the absolute value and it didn't happen that there was a closed form sum for the double sum over the grid, but I still think it's an interesting approach.
The graphic shows the answers for radius = 1, 2, 3 are 5, 13, 29 respectively.
One way to calculate how many there would be is to add 1 for every point on the grid where the distance to the center is greater than the radius, and count how many times that happens checking every grid point. But that's really more of an algorithm...
I found this other way:
For example, this sum totals 113 for r=6 which is the correct value.
It ends up you can always tell from the sign of the y component of this vector whether the point in question is inside or outside of the circle. The X above is the expression for the y component of this vector, derived by calculating the angle to a point from the origin and then finding the polar coordinates of a point that is that same angle from the origin but with a distance to the origin r, of the radius of the circle, and then converting back to cartesian coordinates and looking at the y component. I divide whatever this y value is by the absolute value to get either 1 if the point is inside the circle, 0 if it is on the circle, or -1 if it is outside.
The final expression is totalling these values up and solving for how many must be inside the whole circle from that sum.
Unfortunately it's harder to get rid of the absolute value and it didn't happen that there was a closed form sum for the double sum over the grid, but I still think it's an interesting approach.
Friday, November 1, 2013
Sharing network conjecture
My experiment was to start with a graph with every vertex having a value of 1 and numbered as follows:
The iterative step was to randomly pick a vertex and take a random amount from that vertex and give it to another vertex that the first was connected to. So the first step might be to take .753 from the bottom vertex and give it to the vertex to the top left. Where .753 is just a random amount from the value of the bottom vertex. Then this step repeats on the new values for the vertices.
So I did 3 trials of repeating this step 10,000,000 times on the computer and calculating the average amount that each vertex had throughout the experiment.
Trial one Verices #1 through #6
[1.1518971995357796,
1.1570109780324331,
0.924463843491593,
0.6901779251616574,
0.923239128197964,
1.1532115255805495]
Trial two:
[1.1521431216043976,
1.1542216510411125,
0.9243974762519348,
0.6943663654748421,
0.9220785246649209,
1.1527934609628454]
Trial three:
[1.1496366397190037,
1.1542629725537692,
0.9252708248471094,
0.694030320080955,
0.9233941167266151,
1.1534057260733457]
My conjecture is that the expected value for each vertex V(n) after many iterations is:
V(n) = (n*(1+E(n)))/ (S+n)
Where E(n) is the number of edges connected to V(n) and S is the total number of edges and n is the number of vertices.
So the expected value for the vertices under this formula would be:
[1.1538461538461538,
1.1538461538461538,
0.9230769230769230,
0.6923076923076923,
0.9230769230769230,
1.1538461538461538]
This compares well to the experimental values.
I thought it was interesting that the expected value for a vertex only seems to depend on the number of vertices, the total number of edges, and the number of edges connecting to that vertex, and not on the way that the vertices are connected in the graph.
So I did 3 trials of repeating this step 10,000,000 times on the computer and calculating the average amount that each vertex had throughout the experiment.
Trial one Verices #1 through #6
[1.1518971995357796,
1.1570109780324331,
0.924463843491593,
0.6901779251616574,
0.923239128197964,
1.1532115255805495]
Trial two:
[1.1521431216043976,
1.1542216510411125,
0.9243974762519348,
0.6943663654748421,
0.9220785246649209,
1.1527934609628454]
Trial three:
[1.1496366397190037,
1.1542629725537692,
0.9252708248471094,
0.694030320080955,
0.9233941167266151,
1.1534057260733457]
My conjecture is that the expected value for each vertex V(n) after many iterations is:
V(n) = (n*(1+E(n)))/ (S+n)
Where E(n) is the number of edges connected to V(n) and S is the total number of edges and n is the number of vertices.
So the expected value for the vertices under this formula would be:
[1.1538461538461538,
1.1538461538461538,
0.9230769230769230,
0.6923076923076923,
0.9230769230769230,
1.1538461538461538]
This compares well to the experimental values.
I thought it was interesting that the expected value for a vertex only seems to depend on the number of vertices, the total number of edges, and the number of edges connecting to that vertex, and not on the way that the vertices are connected in the graph.
Monday, October 28, 2013
Rotating linear force
If you made two gears that were parabolas, as one rolls over another a straight line force on one end can multiply the force and rotate it 45 degrees...
Sunday, October 13, 2013
Double centroid line regression
I thought of this way to do a regression of points that is much simpler than the least squares approach, as that involves using the derivative to find a minimal arrangement.
First you have your data points:
Step 1: Find the centroid of the points. This is just averaging the x values and y values of all the points. There are 8 points here so I would add all the x values and divide that sum by 8, and add the 8 y values and divide by 8, to get a point x1, y1.
Step 2: Find the centroid of every point with an x coordinate greater or equal to x1. Here there are 6 points on the graph to the right of x1,y1. So I would sum the 6 x values and divide by 6 and sum the 6 y values and divide by 6. This gives x2,y2.
Step 3: Create the line connecting x1, y1 and x2,y2. Line(T)=x1*(1-t)+x2*(t), y1*(1-t)+y2*(t), for t from a to b, you can choose a and b to make the line as long as you want.
This gives C:
Theorem: This line C has the shortest total of distances squared to the points as measured by the length squared or quadrance of segments from C to all the points, each perpendicular to C.
Proof: Mirror all the points across C making pairs of points adding new points as necessary, C is still the line of balance because the midpoints of all those pairs still lie on C. This doubles the total distance squared to all the points. Then move every point so they all have the same distance squared to C as the average distance squared to C, this doesn't change the total distance squared and C still balances the points because the midpoint of every pair hasn't changed. For every pair of points, the distance to each from C is the same: a. This minimizes the sum of the distances squared to the two points , because if move the midpoint that is on C, to still balance the points it must be on the line connecting the two, but if we lengthen one distance and decrease the other both by c, to maintain the total distance, we have
(a+c)^2 + (a-c)^2 > 2*a^2
because
a^2+c^2+2*a*c + a^2+c^2-2*c*a > 2a^2
because
2(a^2 + c^2) > a^2
for any choice of c .
So since we can only increase the sum of the distances squared to C in this way, the point on C minimizes the distance squared to each pair of points, which means it minimizes the distance squared to any subset of these points because they all have the same distance squared to C. And the original points are a subset of these points so C minimizes the sum of the distances squared to them.
Comparison to Least squares method on sample data
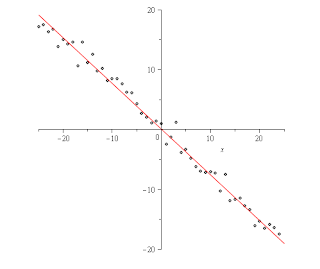
On here is using Maple's least square method vs. the data:
Maple said the linear function should be -.762*x+1/1000.
Here is using this method I made:
My method said the function should be .76*x + .15 (after solving the parametric equation it yields for y in terms of x). So the solutions are both really close but mine ended up a little closer to the function I used to generate the data, I used .75*x+.25 and then added a random amount by picking a random number from a normal with mean 0 and variance 1.
The advantage to using mine versus the standard is that mine is simpler to compute running in linear time vs. the standard method has to solve a matrix which can run in somewhat less than O(n^3) time, so it is much faster taking only the cube root of n as much time. My method doesn't require the points to be one to one with the x-axis, and because it uses a parametric equation the best fit to the data could even be a vertical line whereas that would break the usual method. The axioms needed to use my method are simpler to explain as they only involve basic geometrical ideas and not calculus. And at least in this one test it gave a better approximation of the data than the usual method. I can't think of any disadvantages...
First you have your data points:
Step 1: Find the centroid of the points. This is just averaging the x values and y values of all the points. There are 8 points here so I would add all the x values and divide that sum by 8, and add the 8 y values and divide by 8, to get a point x1, y1.
Step 2: Find the centroid of every point with an x coordinate greater or equal to x1. Here there are 6 points on the graph to the right of x1,y1. So I would sum the 6 x values and divide by 6 and sum the 6 y values and divide by 6. This gives x2,y2.
Step 3: Create the line connecting x1, y1 and x2,y2. Line(T)=x1*(1-t)+x2*(t), y1*(1-t)+y2*(t), for t from a to b, you can choose a and b to make the line as long as you want.
This gives C:
This is your regression.
Theorem: This line C balances the points on either side of C.
Proof:You know the left and right sides with respect to x1,y1 balance because x1,y1 is the centroid. x2,y2 is the centroid of all the points to the right or above and below x1,y1.Imagine another point x3,y3 that is the centroid of all the points to the left or above and below x1,y1. x2,y2 and x3,y3 must balance across x1,y1 because x1,y1 is the centroid and all other points balance at either x2,y2 or x3,y3.. This means there is a line through x1,y1, x2,y2, and x3,y3 because if they weren't collinear x1,y1 couldn't be the centroid of all the points. That line must have the property that the centroid of the points on one side of the line reflect across the line to the centroid of the points on the other side of the line because it passes through the 3 centroids balancing all the points.
Theorem: This line C has the shortest total of distances squared to the points as measured by the length squared or quadrance of segments from C to all the points, each perpendicular to C.
Proof: Mirror all the points across C making pairs of points adding new points as necessary, C is still the line of balance because the midpoints of all those pairs still lie on C. This doubles the total distance squared to all the points. Then move every point so they all have the same distance squared to C as the average distance squared to C, this doesn't change the total distance squared and C still balances the points because the midpoint of every pair hasn't changed. For every pair of points, the distance to each from C is the same: a. This minimizes the sum of the distances squared to the two points , because if move the midpoint that is on C, to still balance the points it must be on the line connecting the two, but if we lengthen one distance and decrease the other both by c, to maintain the total distance, we have
(a+c)^2 + (a-c)^2 > 2*a^2
because
a^2+c^2+2*a*c + a^2+c^2-2*c*a > 2a^2
because
2(a^2 + c^2) > a^2
for any choice of c .
So since we can only increase the sum of the distances squared to C in this way, the point on C minimizes the distance squared to each pair of points, which means it minimizes the distance squared to any subset of these points because they all have the same distance squared to C. And the original points are a subset of these points so C minimizes the sum of the distances squared to them.
Comparison to Least squares method on sample data
On here is using Maple's least square method vs. the data:
Maple said the linear function should be -.762*x+1/1000.
Here is using this method I made:
My method said the function should be .76*x + .15 (after solving the parametric equation it yields for y in terms of x). So the solutions are both really close but mine ended up a little closer to the function I used to generate the data, I used .75*x+.25 and then added a random amount by picking a random number from a normal with mean 0 and variance 1.
The advantage to using mine versus the standard is that mine is simpler to compute running in linear time vs. the standard method has to solve a matrix which can run in somewhat less than O(n^3) time, so it is much faster taking only the cube root of n as much time. My method doesn't require the points to be one to one with the x-axis, and because it uses a parametric equation the best fit to the data could even be a vertical line whereas that would break the usual method. The axioms needed to use my method are simpler to explain as they only involve basic geometrical ideas and not calculus. And at least in this one test it gave a better approximation of the data than the usual method. I can't think of any disadvantages...
Tuesday, October 8, 2013
Beta characteristic and isomorphism
Suppose you have any kind of graph:
Note that some of the edges are weighted, vertices can be connected to themselves, and it doesn't have to be planar. It could also be a directed graph, where the weight from one vertex to another is considered -k times the weight in the other direction for some constant k. A restriction is that if you are treating graphs with multiple edges between vertexes, the weight needs to reflect the number of edges, for example 3 edges between vertexes could be weight 3, and if it's also a directed graph with multiple edges the edges need to be in the same direction. Maybe it's also worth noting that by these conventions a weighted directed graph where all the weights are multiplied by -1 and all the directions are reversed are considered isomorphic.
Consider the labeling of the vertices for the graph pictured above S1:
This is a labeling that is the solution to the following equations:
Every equation is 1 + the sum of the weights of the connections to it's neighbors.
Note that there will always be a solution to this kind of set of equations because these are basically equations for n hyperplanes in n dimensions and it can be seen that none will be parallel because one would have to be a constant plus another but the 1+ on the right hand side prevents that. So the n hyperplanes will always meet at exactly one point, unless it ends up that two or more of the equations were exactly the same, in which case the variables that are free in the set of equations can be set to 0 to get one point.
:
It is the same equations as before except the non 1+ part on the right hand side is divided by 2. For this graph the solution S2 is:
Basically the 1+ on the right hand side of the equations makes sure that equations 1 and 2 aren't linearly related.
Finally make a matrix whose rows and columns are formed by these solutions S1..SN for a graph of n vertices and sort this matrix by exchanging columns until the first row is in increasing order. This gives you what I call the Beta characteristic B(i, j). Note that however the vertices were named in the original graph yields the same Beta characteristic after sorting.
So for a graph of n vertices, I will claim that two graphs are isomorphic if and only if this Beta characteristic is the same.
proof:
First that a Beta characteristic exists and corresponds to one graph:
Let B be the beta characteristic and m(i,j) be variables.
For a graph of n vertices, there are n^2 equations (i,j) and n^2 variables m(i,j)
B(i, j) = 1+(m(1,j)B(i,1)+m(2, j)B(i,2)+...m(n,j)*B(i,n))/i
All of these equations are linearly independent, because every equation has a constant term of 1, no amount of them added together can equal another. And because only the variable part of each equation is divided by i, you can't multiply any two equations by constants and make the same equation. For any choice of m(i,j) there is a unique Beta characteristic B because the equations with left hand side B(i, x) are n hyperplanes in n dimensional space which meet at only one point. Each such point becomes a row in a matrix and these are sorted to become B. For a choice of B there is a unique solution to the m(i,j)'s because there are the same number of equations as variables and they are all linearly independent. These m(i,j) are translated in a unique way to a corresponding graph. .
Second that isomorphic graphs correspond to one Beta characteristic. Isomorphic graphs are only different in the way the vertices are labeled and any labeling of the same graph results in the same Beta characteristic as the columns of the Beta characteristic are always sorted in increasing order of the first row from left to right.
Note that some of the edges are weighted, vertices can be connected to themselves, and it doesn't have to be planar. It could also be a directed graph, where the weight from one vertex to another is considered -k times the weight in the other direction for some constant k. A restriction is that if you are treating graphs with multiple edges between vertexes, the weight needs to reflect the number of edges, for example 3 edges between vertexes could be weight 3, and if it's also a directed graph with multiple edges the edges need to be in the same direction. Maybe it's also worth noting that by these conventions a weighted directed graph where all the weights are multiplied by -1 and all the directions are reversed are considered isomorphic.
Consider the labeling of the vertices for the graph pictured above S1:
This is a labeling that is the solution to the following equations:
Every equation is 1 + the sum of the weights of the connections to it's neighbors.
Note that there will always be a solution to this kind of set of equations because these are basically equations for n hyperplanes in n dimensions and it can be seen that none will be parallel because one would have to be a constant plus another but the 1+ on the right hand side prevents that. So the n hyperplanes will always meet at exactly one point, unless it ends up that two or more of the equations were exactly the same, in which case the variables that are free in the set of equations can be set to 0 to get one point.
:
It is the same equations as before except the non 1+ part on the right hand side is divided by 2. For this graph the solution S2 is:
Finally make a matrix whose rows and columns are formed by these solutions S1..SN for a graph of n vertices and sort this matrix by exchanging columns until the first row is in increasing order. This gives you what I call the Beta characteristic B(i, j). Note that however the vertices were named in the original graph yields the same Beta characteristic after sorting.
So for a graph of n vertices, I will claim that two graphs are isomorphic if and only if this Beta characteristic is the same.
proof:
First that a Beta characteristic exists and corresponds to one graph:
Let B be the beta characteristic and m(i,j) be variables.
For a graph of n vertices, there are n^2 equations (i,j) and n^2 variables m(i,j)
B(i, j) = 1+(m(1,j)B(i,1)+m(2, j)B(i,2)+...m(n,j)*B(i,n))/i
All of these equations are linearly independent, because every equation has a constant term of 1, no amount of them added together can equal another. And because only the variable part of each equation is divided by i, you can't multiply any two equations by constants and make the same equation. For any choice of m(i,j) there is a unique Beta characteristic B because the equations with left hand side B(i, x) are n hyperplanes in n dimensional space which meet at only one point. Each such point becomes a row in a matrix and these are sorted to become B. For a choice of B there is a unique solution to the m(i,j)'s because there are the same number of equations as variables and they are all linearly independent. These m(i,j) are translated in a unique way to a corresponding graph. .
Second that isomorphic graphs correspond to one Beta characteristic. Isomorphic graphs are only different in the way the vertices are labeled and any labeling of the same graph results in the same Beta characteristic as the columns of the Beta characteristic are always sorted in increasing order of the first row from left to right.
Monday, October 7, 2013
Making a rectangle map
So you start with a random map:
Then connect vertexes on the map with straight lines instead of irregular ones, but make sure every region has at least four sides.
Then connect vertexes on the map with straight lines instead of irregular ones, but make sure every region has at least four sides.
Move vertices so every line that is closest to horizontal becomes totally horizontal, same with lines that are closest to vertical, and the rest make 45 degree diagonals.
Imagine the diagonals are the hypotenuse of a right triangle, replace the diagonal with the other two sides of the triangle...
Move vertical and horizontal lines into as few columns and rows as you can while preserving the borders...
This still has the same border information but everything is on a grid....
Can every map be put into grid form? I don't know...
Sunday, October 6, 2013
Cubic sections
I noticed that you can plot the surface of the cone that they use in describing conics as:
I don't know why maple didn't show points close to the origin but they would just follow the same pattern of smaller circles.
So an easy proof that the degree 2 equations are conic sections is suppose you were solving the following two equations, the first for this cone and the second for the plane.
You could in solving these equations add equation 2 to equation 1 and solve equation 2 for z to get these 2:
Then you could plug the expression for z in equation 2 in for z in equation 1
Since a,b,c,d were arbitrary we can group like terms and rename the constant part multiplying each term to f,g,h,j,k,l:
Which is just the general quadratic equation. So the plane intersecting x^2+y^2-z^2=0 are general quadratics, or they could be called conic sections as I wanted to prove.
Now maybe the more interesting thing is that the same reasoning applies equally well to a surface x^3+y^3-z^3=0 intersecting with a plane. It looks like:
Sections of this surface are apparently the cubic sections. Also I believe the reasoning could apply to more variable, but hyperplanes intersecting higher dimensional surfaces.
Thursday, October 3, 2013
Cooling matrix revisited
I noticed if you have a grid of temperatures matrix T like:
The diagonal ellipses are meant to imply that the grid can go on to any number of rows and columns...
I found this matrix A:
which is meant extend to however large the temperature grid is. If your temperature gird is at time t then this formula:
finds the temperatures in your grid after 1 second where k is the usual physical coefficient in Newton's law of cooling. It works best if the area you are concerned about is far enough from the boundary of the temperature matrix that the values in the first and last column and row of the matrix don't begin to affect the area you are looking at.
Reasoning:
Look at what happens to a cell T[i,j](t) in the temperature matrix at least one row or column away from the edges of the matrix. After applying the formula the value in that cell becomes:
T[i,j](1) = k*(T[i,j](0) - (1/4)*(T[i-1,j](0)+T[i+1,j](0)+T[i,j-1](0)+T[i,j+1](0)))
So the temperature changes by a proportion k times the difference between the temperature of the cell and the average temperature of the cells around it. This is exactly as it should be by Newton's law of Cooling.
The diagonal ellipses are meant to imply that the grid can go on to any number of rows and columns...
I found this matrix A:
Reasoning:
Look at what happens to a cell T[i,j](t) in the temperature matrix at least one row or column away from the edges of the matrix. After applying the formula the value in that cell becomes:
T[i,j](1) = k*(T[i,j](0) - (1/4)*(T[i-1,j](0)+T[i+1,j](0)+T[i,j-1](0)+T[i,j+1](0)))
So the temperature changes by a proportion k times the difference between the temperature of the cell and the average temperature of the cells around it. This is exactly as it should be by Newton's law of Cooling.
Wednesday, October 2, 2013
fertilizer from sunlight
So I thought, have a pond that grows algae, the algae use water and sunlight to create carbohydrates, feed the algae and water to a tank of yeast, the yeast eat the carbohydrates and produce alcohol, keep the alcohol and feed the dead yeast to bacteria, the bacteria eat the dead yeast to produce methane, keep the methane, and the dead bacteria can be used as fertilizer for plants. So from sunlight and water you get alcohol and methane some of which is used as fuels to drive the pumps that feed from one tank to another and you end up with fertilizer.
separating noise from information in a picture
Suppose you have a picture like:
It seems to work as an edge detector...
It's easy for a person to tell where the two interesting objects are in this picture but I found a way for the computer to do it as well.
Step 1: Make a new image where you look at each pixel in the original image and add up how far it's value is from it's neighbors. If it is exactly the same color as all it's neighbors that is a 0 if every surrounding pixel is exactly the opposite color that is a 255 (this means white in computer graphics).
This has the effect of making all contiguous areas of color or gradients solid black.
Step 2:Make a new picture where the new pixels are the average of the old pixels and their neighbors. Sort of a blur.
Step 4. Blur again but only keep pixels that are between 0 black and 128 grey, everything else is made white.
Now do the same thing again but only keep pixels that are between 0 black and 64 grey. All else stays white.
Now you should have a nice binary map of where the interesting parts of the original picture are with the noise removed.
So it's kind of interesting to see what this process does to normal pictures...
Tuesday, October 1, 2013
3d keyboard
My idea was that there would be this ball with buttons on it for all the keys on a keyboard inside each triangle and the triangles stick out a bit so you can hold it easily without pressing any on accident, you press inside each triangle for the key and a little harder to do shift+the key. So you could type using only one hand while the other one does the mouse is the idea. I don't know what the learning curve would be like or if people could get pretty good at it or whether it would just drive anyone insane that tried to use it lol.
maybe a better idea than the last thing, this is a ball you hold in your fist so your fingertips are on the five buttons, and it has a gyroscope in it so it can tell which way you are holding it in space like an ipad. And depending on which way you rotate it, it changes what the five buttons do.Like in one position the five buttons could be e,t,a,o,space, and if you rotate it a bit in a certain direction they change to n,s,h,i,backspace.
maybe a better idea than the last thing, this is a ball you hold in your fist so your fingertips are on the five buttons, and it has a gyroscope in it so it can tell which way you are holding it in space like an ipad. And depending on which way you rotate it, it changes what the five buttons do.Like in one position the five buttons could be e,t,a,o,space, and if you rotate it a bit in a certain direction they change to n,s,h,i,backspace.
Sunday, September 29, 2013
Graph Isomorphism matrix
If you have a graph like:
Note that some of the edges are weighted, one vertex connects to itself, and one connection can cross another.
We can associate a connectivity matrix M with this graph like so:
Note that some of the edges are weighted, one vertex connects to itself, and one connection can cross another.
We can associate a connectivity matrix M with this graph like so:
Here, there is a in cell (x,y) if x and y are connected and the weight if any replaces the 1.
Also a permutation matrix of the same size can be defined as any matrix that has one 1 in every row and every column, for example:
A nice theorem about these matrices is that if two graphs are isomorphic we can write:
P*M*P = N
where M is the connectivity matrix of graph M, and N is the connectivity matrix of graph N, and P is any permutation matrix.
Proof:
P*M*P is the matrix you get when you first permute any number of rows of the matrix, and then do the same permutation on the columns. And this is exactly the same as taking the graph associated with the connectivity matrix and permuting the labeling any way. And of course two graphs are isomorphic if there is a way to permute the labeling so that you generate the same connectivity matrix.
This isn't an if and only if because I found two non-isomorphic graphs that are related in this way by a permutation matrix.
Friday, September 27, 2013
maybe spacetime under gravity?
I found this nice relationship between the unit circle and a distribution I name in the picture...
In words it is a distribution that is tangent to the circle at 0*, and has the same area as the circle from -infinity to infinity. So it's pretty interesting on it's own but I found it thinking about how relativity is always explained as how mass warps spacetime like a ball on a rubber sheet. I had the idea that maybe a unit mass of a unit area displaces a unit area of spacetime from minus infinity to infinity. I don't know enough differential geometry to say whether this fits with the very complex relativity formulas or not but it was just a thought.
IMPORTANT NOTE:
The area of the formula for the green region from minus infinity to infinity is pi, but subtracting the bottom half of the circle's area of pi/2 gives pi/2. As I'm considering it as a displacement it makes sense this way.
* Dr. Rose helped me with this part I originally though it stayed tangent to the circle over an interval...
IMPORTANT NOTE:
The area of the formula for the green region from minus infinity to infinity is pi, but subtracting the bottom half of the circle's area of pi/2 gives pi/2. As I'm considering it as a displacement it makes sense this way.
* Dr. Rose helped me with this part I originally though it stayed tangent to the circle over an interval...
Monday, September 23, 2013
Rough modeling of rows of Pascal's triangle as a distribution
I found a rough correspondence between the formula under the Consider: and Pascal's triangle...
Also, one can solve for the middle number approximately:
for r = 11
the right answer is 252 so pretty close.
One practical reason for this approach is for example finding the middle number of row r of pascal's triangle, ordinarily you would use the combinatoric formula r!/((r-1!)*(r!)) but eventually the factorial involves numbers too large for Maple to calculate, but using my integral formula for the middle number only involves calculating 2^r which it can do more easily.
Sunday, September 22, 2013
Friday, September 20, 2013
different unit circle
Maple surprised me when I asked it to graph this:
It's provable pretty easily from Euler's formula:
e^(pi*i)=-1
(e^(pi*i))^x = (-1)^x
(-1)^x = e^(pi*i*x)
I think it's kind of a nice notation for the unit circle on the complex plane because you don't have to write all the e's,pis, and i's everywhere. And it's easier to work in then radians, for example (-1)^(22.4) is obviously the same as (-1)^(.4) when you mod it by 2 which is .4 of the way to the left of the circle after going around 11 times.. But e^(22.4*i) you would have to think modulo 2*pi which might not be that obvious. It ends up that is 3 times around the circle and .5 of the way to the left of the circle....
I
Subscribe to:
Posts (Atom)

.jpg)