ith n gonal and ith m gonal number add to the ith N+M-2 gonal number

The basic idea here is if you take the ith N-gonal number and the ith M-gonal number and join them along one side, so that the total number of dots is the number in the n-gonal number + the number in the m-gonal number minus i dots that overlap, you have the same number of dots as in the ith N+M-2 gonal number...

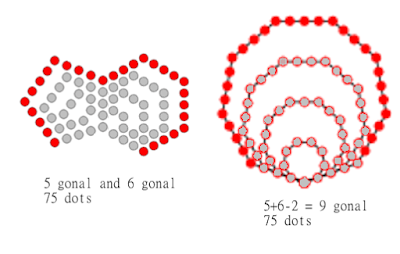
One other simple case is a triangular number and a square number adding to a pentagonal number, because 3+4 -2 = 5, below with i=2:

 **Proof**

The top 2 lines are the formula for the number of dots in the ith n-gonal and ith m-gonal number and the third line is for the ith M+N-2 gonal number, then note that an i has to be subtracted from the first two to equal the third...