Note that there is a largest a*n! for a from 0 to n smaller than X:
here
X=443.125
and a =3 and n = 5
3*5*4*3*2 = 360
because 4*5*4*3*2 = 480 which is larger than X
any a times n=6 6*5*4*3*2 is too large and a=4 and n = 4 is 4*4*3*2=126 is too small
So we consider the a=3 in front of 5*4*3*2 to be the first digit
3
Now X-360 = 83.125 so we iterate:
that is a=3 times n=4 4*3*2 = 72 and again a =4 would be too large and 3*3*2 is too small
so the second digit is 3
3
83.125 - 72 = 11.125
just one 3*2
1
5.125
two 2's
2
1.125
one 1
1
.125
Now the factorials invert the above is 0 1/2's
0
.125
And also 0 1/2*3
0
.125
And 3 1/4*3*2
3
0
So the number can be written as 3,3,1,2,1x0,0,3 where x is the radix point (decimal point but more general)
which to go back to decimal is:
Every number can be transformed into this "factorial base" number where the possible size of the digits increases by 1 further to the left and the right of the radix point, uniquely, except for the usual caveat that 0,0,3 is the same as 0,0,3,3,4,5,6...
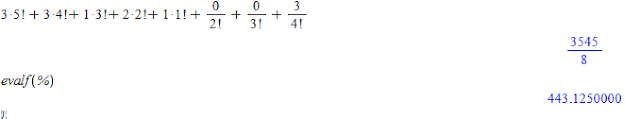
No comments:
Post a Comment