Lattice for nearest neighbor

Supposing you have some metric space with well defined midpoints, here just a plane with points...

Start making a latice by picking a point to be the root...

Now pick another point and make it a child...

The general rule for adding another point is:

For a parent G with children {A,B,...} and a point k to be sorted, there are 4 things that can happen, in order of precedence:
1. k is closer to the midpoint of G and and one or more X,Y... of {A,B,...};  than the midpoint is to either G or X
or
2. k is closer to G than it is to any X of {A,B,...}
or
3. k is closer to the midpoint of two of G's children, X and Y,  than it is to either of the children in question
or
4. k is closest to one of the children X

and what you do for each case is:
1. remove X,Y... and any of their children from the tree and replace with k
2. add k as a child to G
3. take X and Y as parent nodes and repeat the process placing k somewhere under both
4. restart the process starting with X as the parent node

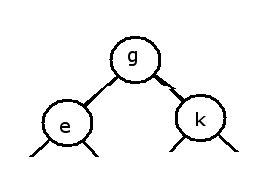
So for the example given:
1. k is not closer to the midpoint of G and E than either G or E
2. k is closer to G than it is to E
so we do 2 and make k another child of G

Now considering point b, we get all the way to rule 4, and make the new parent node E and continue with rule 2 adding b as a child of E.

Now considering point d, we would need rule 3 and make d a child of both e and k... Sometimes you will have to write it in the tree as two nodes but here we can draw it as one with 2 parents easily...

In the end you end up with a lattice where every node is closest to one of it's parents or one of it's children... 

** To be added**

I'll write some source code and post some results with big maps...