Beta sub t, binary comparison between x and y

I've defined this function:

Where x and y are binary variables. And mod indicates the remainder of it's first argument when divided by it's second. The interesting thing about this function is to consider a certain truth table between x and y:

This could be considered !(x xor y) in the usual computer terminology, thought that starts to show how confusing the naming can be.
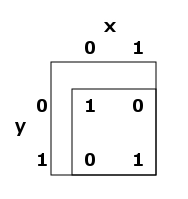
To see what Beta(t) does first look at the truth table read across as rows 1 0 0 1, this is the binary number 9, so we have:

First look at the function at x=0 and y = 0, the percent sign means maple uses the last result in place of the percent sign:

In general this Beta function at t produces the 0-15th truth tables for comparing x and y.  So to get the truth table that reads across by rows as 1 1 0 0, that is 12 in binary so you would look at B(12) at x = 0..1 and y = 0..1

**Explanation**

Note that the function in x,y over x=0..1 and y=0..1 is:

19*t+19 for t = 0..15:

19

38

57

76

95

114

133

152

171

190

209

228

247

266

285

304

These numbers above mod 17

2

4

6

8

10

12

14

16

1

3

5

7

9

11

13

15

Then the above mod 2:

0

0

0

0

0

0

0

0

1

1

1

1

1

1

1

1

The other four squares in the matrix go 0000111100001111, 0011001100110011, and 0101010101010101

so you get every combination in order...for example the 13th place in each of these four binary numbers is:

1,1,0,1 or 1101 which is the number 13 in binary...