Recursive tree for numbers that add and multiply to the same number

Setting up two equations for two numbers that both add and multiply to k and using the quadratic formula yields:

For example if k=10, this yields: 8.2459 and 1.1270, which both add to 10 and multiply to 10. 

It can be seen that any number less than 4 provides two imaginary solutions. But it's possible to make a tree of just the real solutions by stopping anytime you get below 4...

So 1.127, 1.148, 1.180, 1.231, 1.336 and 3.976 both sum to 10 and all multiplied together equal 10. 

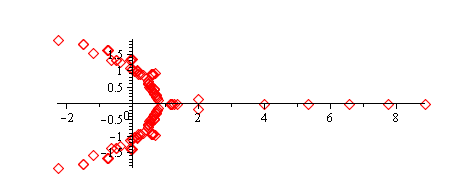
But if we don't ignore complex numbers we get and produce two child nodes for each parent node in the tree, the bottom row or the 5th generation looks like this on the complex plane:

All the nodes on the whole tree look like this:

after 7 generations:

There's some really interesting structure to this tree on the complex plane, but I'm not sure what to make of it.