This substitution for x in an integral:
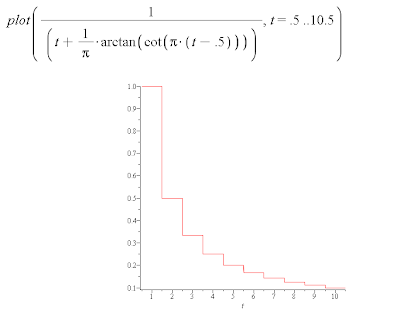
which has a graph of:
Makes this relationship true:
For example say f(x) was 1/x and we are interested in bounds from 1 to 10.. substituting in the expression for t in for x in 1/x and plotting shows:
You can see that the integral over this region is going to be related to the sum trivially.
Alternatively, x(t) can be written as an infinite Fourrier series which sums to a complex exponential function:
x(t)
as a check a plot of this bottom function:
So in particular the zeta function can be rewritten as an integral by substituting the complex exponential formula into the integral/sum relationship first mentioned and simplifying:
Unfortunately Maple didn't know what this integral evaluates to! :)
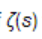
No comments:
Post a Comment