I found this function:
as A get's larger this function get's closer and closer to the true value. For instance:
whereas the sum on the left by itself is only:
So the integral appears to be adding very close to the right amount.
and making A larger...
where the Ci function is:
And the gamma constant is:
Now back to the original formula I found:
There is a simple reason why it works... the integral of cos(pi*x)^2 from an integer minus .5 to that integer plus .5 gets closer and closer to 1/2 for larger integers. So a function you multiply it by is made like a discrete sum over the integers divided by 2. It is actually a handy way to convert from a discrete sum to an integral that I'll probably go more into in the future.
The example for k=3...
So the integral is adding something around .02 and getting a lot of decimal places correct.











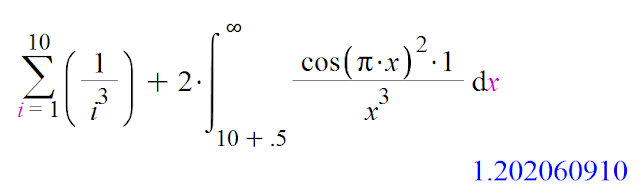
No comments:
Post a Comment