
I've derived this equation for a kernel about the point (a,b) on the plane where M is the peak magnitude, k is a constant that depends on the material, and t is of course time.
A graph at that point in time is:
Now I imagine that the heat over the plane starts off as a function T(x,y) let's say it is this function:
So we have a dome of heat.
I'm imagining that the amount of heat from every point on this function spreads according to the kernel and is integrated like so:
The amount of heat at point (x,y) is the sum of all the kernels of heat around every other point on the plane.
M in the equation is T(x,y) and (a,b) is anywhere within the square (v,w) (p,q)...
So if k is 1 and t is 1 and T(x,y) is the function given, then:
which Maple still can't solve for the general (x,y) so we would have to look at a particular x,y like -3,2
In my original plot some of the temperatures were negative.
So anyway this gets pretty computationally expensive as you solve for every point on some grid of (x,y) values, but in the end you would have an approximation of the heat map after t seconds.
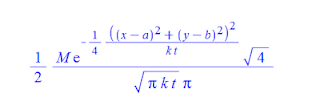






No comments:
Post a Comment