You can see that this equation always holds no matter the a. So you can do something like the following to figure out the square root of a number, here for example is finding the square root of 10 using the top formula:
Thus there is one general continued fraction expression for every square root.
Normally the discussion of continued fractions explores each square root as having a different form, such as on wikipedia http://en.wikipedia.org/wiki/Square_root
The have tables of how this looks for every different possible square root:
But this idea I've had gives the same form for every square root.

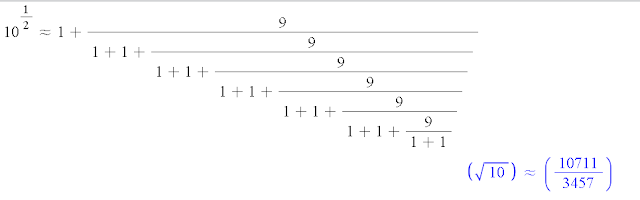


If A is the closest integer root to X and B=(X - A*A) then A plus (B over (2A plus (B over (2A ...)))) is another form. It has the advantage over yours that for general numbers it doesn't have to consume as many pairs in order to start emitting terms. But it has the disadvantage that you still need an integer square root to get started, whereas yours does not have this preliminary calculation.
ReplyDeleteOf course, if I were to always estimate the integer square root as "1", well... you be the judge if our continued fractions are then the same. :)
I was looking for a sequence of rational numbers converging to a square root, and your example is straightforward.
ReplyDeleteWONDERFUL... I like to contact you always
ReplyDelete