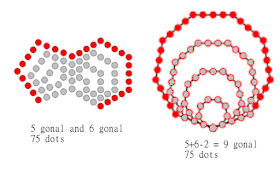
One other simple case is a triangular number and a square number adding to a pentagonal number, because 3+4 -2 = 5, below with i=2:
The top 2 lines are the formula for the number of dots in the ith n-gonal and ith m-gonal number and the third line is for the ith M+N-2 gonal number, then note that an i has to be subtracted from the first two to equal the third...


No comments:
Post a Comment