This represents the line from (x1, y1) to (x2, y2) and we give it an initial value:
Then you have a recurrence relationship over the previous 4 variables like this:
P1 under the recurrence goes to:
And then:
Of course there are infinitely many possibilities for the recurrence grid formulas I just thought this was a nice one...
**For general n-gons**
The general recurrence extending the one above for octagons with theta =pi/4 to a general case is:
So a pentagon would use a theta of 2*pi / 5, etc... Constants multiplying the bottom 2 entries of the recurrence grid make various sorts of spirals
Just a random example:
The first 7 lines generated:










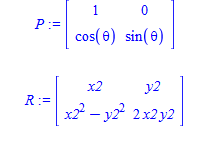


No comments:
Post a Comment