So you can use it to solve certain problems like what if you go 1/5th of the way from point (3,5) to point (-4,2) along a circular arc? The circular arc connecting the two points is:
**Solving for angles between unit vectors**
Another thing to do is say we have the unit vector ((2^1/2) / 2, (2^1/2) / 2), and we want to know the angle between that and ((3^1/2)/2), (1/2)) we can first make a circle with that start point and negative times each coordinate as the final point like so:
It's pi/12 between those two vectors... If the angle had been the same but counterclockwise it would have read as -pi/12!





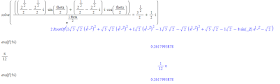
No comments:
Post a Comment