First consider that you have the basic 2nd degree polynomial:
That can be written as a parametric equation vector:
And you can also consider a linear transformation matrix like so:
Multiplying the vector by the matrix gives a new parametric vector:
Which after solving for t and plugging into the y component is transformed back into a standard polynomial:
So for example if you have a target polynomial (random):
By setting the coefficients equal to the last equation, hat creates 3 equations with 3 unkowns:
These can be solved for a, b, c:
So the transformation matrix is:
This is the linear transformation matrix to convert the parabola x^2+x+1 to 5x^2-2x+3
So it is pretty easy to see that every possible parabola is the basic parabola times a linear transformation matrix that it is possible to solve for.
I believe but I'm not sure that it can apply to polynomials of any degree but you have to add more degrees of freedom to the transformation matrix; like for cubics:
A transformation matrix like the above should give 4 equations with four unknowns, etc.









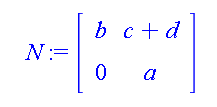
No comments:
Post a Comment