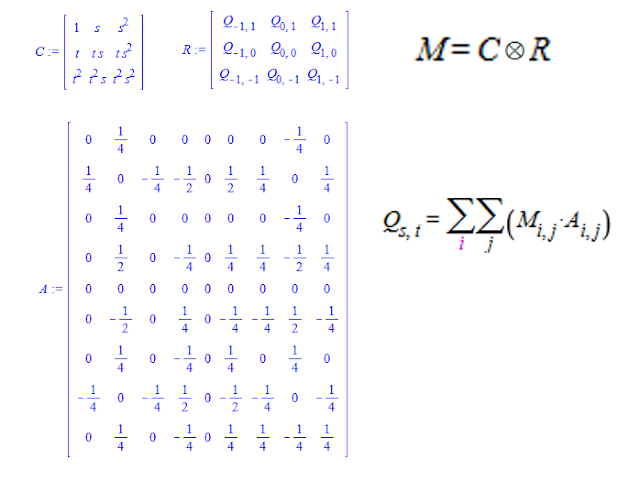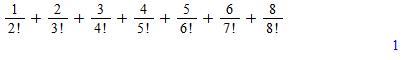Q(s,t)
Note that the same formula applies first to the x coordinates, and then to the y coordinates and can work in any number of dimensions 2 or greater, Imagine that Q can be any of X, Y, Z component axis, and s and t vary continuously from -1..1... I'm not sure if there might be a notation using summations or matrices that makes this simpler and nicer to write, but maybe it's not that big of a deal when you can just write Q(s,t) to mean this in other formulas... It can also be fairly easily extended to volumes or higher dimensional objects using more variables than just s and t....
It's derived from my earlier post on the E_Bezier:
http://benpaulthurstonblog.blogspot.com/2015/12/ebezier.html...
One can derive something in a similar way from regular Beziers but then the mapping isn't conformal...
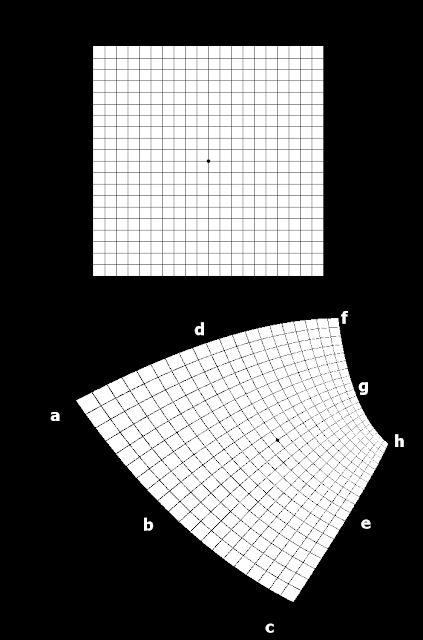
I made s and t vary from -1..1 so they can shrink to -delta +delta around a point on surface F for a sort of surface approximation, it can be shown that as delta shrinks to 0 in the limit the result is F at that point..Or to make the Q values closer and closer to surface F at a point to get a sort of parameterized surface derivative or tangent surface ( I think! I might explore that in a later post)... Also parameterization is a natural fit for conformal mappings because they are both scale and translation-invariant (also rotation)... A rectangle under a conformal mapping can be achieved by adding a coefficient multiplying one of or both t and s,.
http://benpaulthurstonblog.blogspot.com/2015/12/ebezier.html...
One can derive something in a similar way from regular Beziers but then the mapping isn't conformal...
I made s and t vary from -1..1 so they can shrink to -delta +delta around a point on surface F for a sort of surface approximation, it can be shown that as delta shrinks to 0 in the limit the result is F at that point..Or to make the Q values closer and closer to surface F at a point to get a sort of parameterized surface derivative or tangent surface ( I think! I might explore that in a later post)... Also parameterization is a natural fit for conformal mappings because they are both scale and translation-invariant (also rotation)... A rectangle under a conformal mapping can be achieved by adding a coefficient multiplying one of or both t and s,.
I think maybe General Relativity might be simpler rewritten with this type of formula in mind, because it seems like the complicated thing is keeping all the axis components sorted out whereas this you can do each variable individually with the same formula, just a guess though I don't know that much about General Relativity...
**Matrix version**
Or using matrices instead of the row and column vector and the tensor product:
**Python Program**
It's more convenient to use a bit different formula when doing things with computer images, ... It's the function q in the program below and the program takes any image of any size and maps it according to the following, there's also a variable for a value for oversampling; this one below is 2*x oversampled...: This map was actually made with the program, you can see the grid lines only ever cross at right angles, that's the conformal property...
**Python Code listing (using Pillow for python)**
from PIL import Image
def q(s,t,a,b,c,d,e,f,g,h):
p = 1.0*((1/4)*b-(1/2)*s*b+(1/2)*s*s*b+(1/2)*t*t*d+(1/2)*t*d+(1/4)*e+(1/4)*g+
t*t*s*s*((1/4)*g+(1/4)*b+(1/4)*d+(1/4)*e)-(1/2)*t*t*s*g+(1/2)*s*s*g+
(1/2)*s*g-s*s*((1/4)*g+(1/4)*b+(1/4)*d+(1/4)*e)-t*t*((1/4)*g+(1/4)*b+
(1/4)*d+(1/4)*e)-(1/2)*t*t*s*s*e+(1/2)*t*s*s*e+(1/4)*t*s*f+(1/4)*t*s*s*f+
(1/4)*t*t*s*f+(1/4)*t*t*s*s*f-(1/4)*t*t*s*c-(1/4)*t*s*s*c+
(1/4)*t*t*s*s*c+(1/4)*t*s*c-(1/2)*t*t*s*s*g-(1/2)*t*e+(1/2)*t*t*e-
(1/2)*t*t*s*s*b+(1/2)*t*t*s*b+(1/4)*d-(1/2)*t*s*s*d-(1/2)*t*t*s*s*d+
(1/4)*t*t*s*s*a-(1/4)*t*s*a-(1/4)*t*t*s*a+(1/4)*t*s*s*a-(1/4)*t*s*s*h+
(1/4)*t*t*s*s*h+(1/4)*t*t*s*h-(1/4)*t*s*h)
return p
def main():
grid = Image.open("grid.png")
output = Image.new("RGB", [700, 1200])
w, h = grid.size[0], grid.size[1]
c = [[116, 724],[288,926],[477,1059],[354,622],[579,897], \
[552,588],[582,717],[634,796]]
print(w,h)
oversample = 2
for i in range(0, oversample*w):
for j in range(0, oversample*h):
s = (2.0/w)*(i/oversample*1.0)-1
t = -((2.0/h)*(j/oversample*1.0)-1)
color = grid.getpixel((i/oversample*1.0,j/oversample*1.0))
px = q(s,t,c[0][0], c[1][0], c[2][0], c[3][0], c[4][0], c[5][0], c[6][0], c[7][0])
py = q(s,t,c[0][1], c[1][1], c[2][1], c[3][1], c[4][1], c[5][1], c[6][1], c[7][1])
px = int(px)
py = int(py)
try:
output.putpixel((px,py), (color, color, color))
except:
print((i,j), (px, py))
output.save("conformal.png")
main()