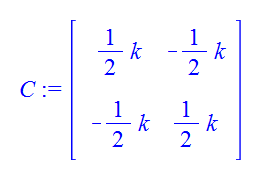Parametric Linkage Kinematics

Considering a machine like this:

As the point on the unit circle R2 goes around the block P4 slides up and down in it's channel.

Most treatments I've read say the follower will move up and down as a sine wave, but it's possible to be more exact...

 Let's say for example it's a unit circle centered at the origin and the channel is on the y axis...

First the point on the circle is parameterized like so:

Now parameterize with the same parameter the motion of the block P4:

This means the block is not moving in the x direction and it is moving some function f(t) in the y direction. 

Also, let's say the length of the coupler is 5. Then we know that the distance between C and P is 5 or:

Now we can solve for f(t) which ends up having 2 solutions. 

One of these corresponds to P arranged above the circle and the other below. Not the difference between these solutions and a sine wave... 

Another example might be the four bar linkage:

We can parameterize point B. 

where k(1), k(2), etc.  are the lengths of the connectors of A,B, C, D. 

 C is also parameterized but in general it will be to a different variable s and if A is at the origin then D will be offset to a point (x,y). 

The distance between B and C is k2 so:

Let's say k1 was 3, k2 = 4, and k3 =5 and (x,y) is the point (3,2)

then 

It's messy,but on a computer this can be solved for s and plugged back into the parametric equation for point C. Here's an animation of how C moves as T goes linearly from 0 to 2*pi. 

This animation shows the possible range of C, which is along a circle, though an anomaly in the graph shows a jump from one point on the circle to another. 

heron matrix

I found this formula for finding the area of a triangle of sides length a,b,c; basically I started with Heron's formula and found a matrix multiplication that produces what would ordinarily be under the square root.

(After you add all the cells in the resultant matrix)

Deriving a cooling matrix from Newton's Law of Cooling

This is an improvement on the last blog entry inspired by a suggestion from Dr. Rose.

Suppose you start with a grid of temperatures like this:

Newton's law of cooling says that an object cools at a rate proportional to the difference of temperatures between itself and its surroundings.
So just considering that this grid is connected everywhere but the diagonals, the cell with starting temperature a would be expected to cool like:
T(new) = a-(k*(b-a) + k(c-a))/2
In other words the value of a cools proportionally to the average of the differences between it's surroundings and itself.

I introduce this matrix:

Now consider the following procedure: A-(A*C+C*A)

So the top left cell and the others are equal to our formula:
T(new) = a-(k*(b-a) + k(c-a))/2
 = a- ((.5)*kb -.5ka) +(.5kc - .5ka)
then grouping the ka terms
=a-ka +.5kb +.5kc

Now as for the fact that this doesn't consider cooling across the diagonals, what will happen is after one time step the top left corner and the bottom left corner cool towards each other, and then the next time step the new temperature in the bottom left corner will cool the bottom right corner, so actually information from the top left corner does reach the bottom right corner it just takes an extra step.


Also the sum of the four cells conserves the total temperature:

Cooling matrix

Suppose you have a grid of temperatures such as:

I found this matrix C:

The interesting thing about C is when you do this operation: 

(matrix multiplication)

For the example matrix I gave A, this gives: 

The sum of all of these entries is exactly the same as the sum of all the entries in matrix A! 

If you look at matrix A and the resultant matrix you can see that every cell gets closer to the average value of all the entries in the matrix, which is what you would expect from a grid of temperatures settling into an average temperature. 

Let's look at the bottom right cell in A, that starts off at 7 and goes to 4.875, another application of the matrix multiplication with C gives: 

7

4.875

4.1406

3.83

3.673

3.584

3.531

3.498

3.478

...

You can see it is is sort of exponentially decaying to the average temperature of 3.444

Math of Speech

  To make a sound for speech you move how open your mouth is, where your tongue is in your mouth, how rounded your lips are, whether your vocal cords are vibrating, and if so what tone in your vocal range they are producing. Every syllable has a beginning, middle and end time period where you move from one combination of all those variables to another, and then to a final state.
   So going through these let's call how open your mouth is M(m) where m can be a number from 0 to 6, with 0 closed and 6 fully open. The tongue can be at a position T(f, u) where f is how forward the tongue is and u is how far up in the mouth it is. A good range is f can be from -2 to 2 for all the way back to all the way forward and u from 0 to 2 for bottom middle and top of the mouth. Lips could be L(l) with l from 0 to 1, for not at all rounded to fully rounded. And vocal cords could be V(o, t) with o being binary 0 or 1 off or on, and t from 0 to 1 for the lowest to highest pitched tone you can make. And B(b) is whether your breathing out or not.
   So a part of a syllable looks like:
M(m), T(f, u), L(l), V(o,t)
  And a whole syllable looks like:
M(m1)    -> M(m2)    -> M(m3)
T(f1,u1) -> T(f2,u2) -> T(f3,u3)
L(l1)    -> L(l2)    -> L(l3)
V(o1,t1) -> V(o2,t2) -> V(o3,t3) 
B(b1)    -> B(b2)   -> B(b3)
For instance the syllable "boy?" where the question mark means the tone rises as you go through the word...
M(0)     -> M(3)     -> M(3)
T(2, 0)  -> T(1, 0)  -> T(1, 0)
L(1)     -> L(.5)    -> L(0)
V(1, .5) -> V(1,.75) -> V(1, 1)
B(1)     -> B(1)     -> B(1)
This basically means the mouth is going from closed to half open, the tongue goes from all the way forward on the bottom of the mouth to just a bit back still on the bottom, the lips go from rounded to not-rounded, and the voice is on and goes up in tone. 

A different example might be "swipe"
M(3)     -> M(1)     -> M(0)
T(1, 2)  -> T(1, 1)  -> T(1, 1)
L(0)     -> L(0)     -> L(0)
V(1, .5) -> V(1,.75) -> V(0, 0)
B(1)               ->    B(1)               ->    B(1)

So really a syllable is pretty complicated...  

The perfect Display

I imagine this display might be possible someday. There are three main things you do with LCD screens, viewing content abstractly related to looking at a piece of paper, tasks related to producing those or using other programs and watching movies. Here are the relevant aspect ratios:

So you see on the top left is the typical U.S. paper size 11x8.5, but I left enough space around it to handle the standard the rest of the world uses A4... But in some bizarre mathematical coincidence A4 is the perfect size to fit a U.S. standard size into and have room for all the toolbars and scroll bars and everything.
   The HDTV's now are 1.77:1 aspect ratio. But the movies you see in the theater are 2.39:1, A4 is 1.414:1 so two longways is 2.8:1.  So the idea is you would have two screens the A4 size, that you could put side by side so you can work on two different things full size but then you rotate both of them and put them side by side to go into movie mode. Unfortunately there are still black bars around the movie but this is the best I could do. And Hollywood historically has always gone to wider and wider screen 2.39:1 is the current that I used above.
  The big technical hurdle is making an lcd without a bezel, I found one 40 inch HDTV that the bezel was only four pixels wide (which would still be annoying going down the middle of the display) but that TV was 5000 dollars so right now it is expensive to do but hopefully this will be possible someday...
   I call the screens "Foils" so someone can say "Lock Foils into Movie position!"

***UPDATE***
A friend of mine, Blair Updike, suggested using projectors instead. The image projected doesn't have the limitation of the bezel around the lcd and I believe that makes it possible a lot sooner than what I had in mind. The projector would basically be two projectors built in one case that can rotate and move what they are projecting from one mode to the other.

gclamps

These are supposed to lock tight like the mechanism on the gas pump.